人工智能考试期末复习
但愿看我博客复习的同学不会被8%的概率dropout吧~
AI的四大主流流派
- 符号主义(Symbolism)例:知识图谱
- 连接主义(Connectionism)例:深度神经网络
- 行为主义(Behaviourism)例:机器人
- 统计主义(Statisticsism)例:机器学习
AI、机器学习、深度学习三者之间的异同和关联
- 三者属于包含关系:AI包含机器学习,机器学习包含深度学习,深度学习主要指机器学习中的深度神经网络;
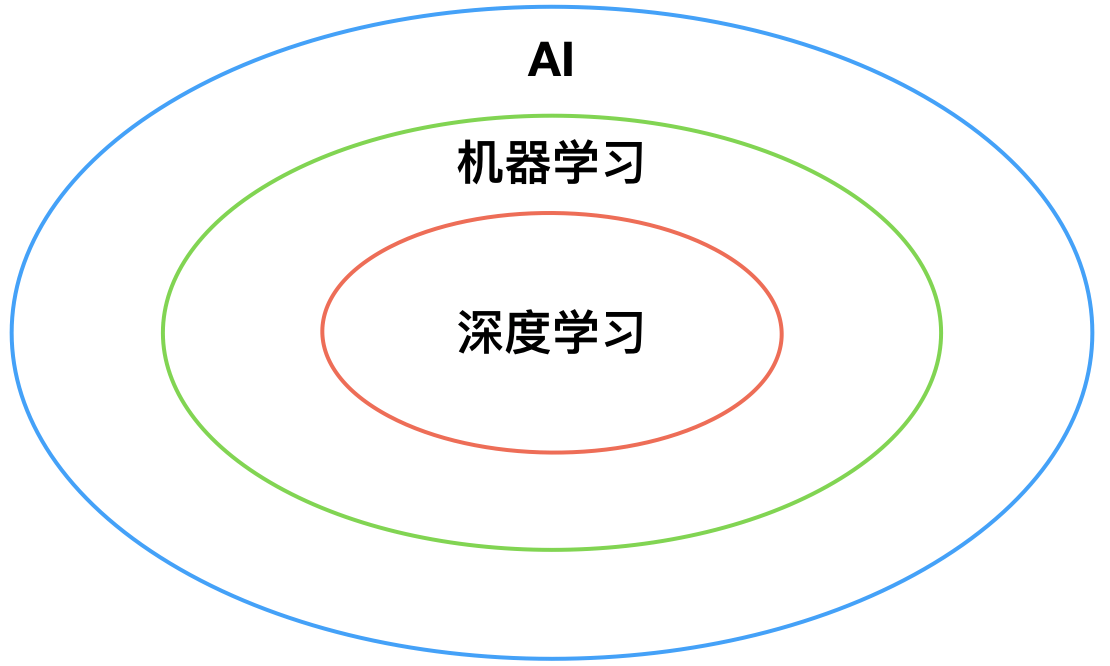
在机器学习中,需要先进行人工特征提取,再定义Model;而大部分深度学习只构建一个端对端的模型,没有人工特征提取;
在深度学习中,有时需要先进行数据清洗、格式转换、特征提取(卷积)等操作,再将数据喂给全连接神经网络。
机器学习的两个阶段
训练:“三步曲” on training set
定义Model;
定义Loss/cost/error/objective function;
如何找到Model中的最佳function:利用梯度下降来迭代调整参数,以使得损失函数达到最小值。深度神经网络通过反向传播来降低损失,优化模型。
预测:on Devset and testing set
- 前向传播:预测输出,计算Loss;
- 通过开发集(Devset)可以用于超参数调优,模型经过训练集训练,和开发集调优,然后交给测试集测试性能。
几个基本概念:
- Epoch:对整个数据集进行一次forward和backward过程,被称为一个Epoch;
- Batch_size:一次forward/backward过程中的训练样例数,被称为Batch_size;
- Batch:使用训练集中一小部分样本对模型权重进行一次反向传播的参数更新,这一小部分样本被称为一个Batch;
- Iteration:1个Iteration等于使用batchsize个样本训练一次。
举个栗子🌰:假设我的训练集中总样本数为2048、Batch_size=128,那么我需要迭代(Iterations)16次才能完成一个Epoch。
机器学习分类的定义及差异
监督学习
监督学习的目标是建立一个学习过程,将预测结果与“训练数据”(即输入数据)的实际结果进行比较,不断的调整预测模型,直到模型的预测结果达到一个预期的准确率。
例:手写字符识别、肿瘤分类、预测天气、支持向量机、线性判别。
特点:训练样本数据和待分类的类别已知,且训练样本数据皆为标签数据。
非监督学习
非监督学习从无标记的训练数据中推断结论,它可以在探索性数据分析阶段用于发现隐藏的模式或者对数据进行分组。
例:聚类分析、主成分分析。
特点:训练样本数据和待分类的类别已知,但训练样本数据皆为非标签数据。
半监督学习
半监督学习的训练数据通常是少量有标记数据及大量未标记数据,介于无监督学习和监督学习之间。
例:聚类假设、流形假设。
特点:训练样本数据和待分类的类别已知,然而训练样本既有标签数据,也有非标签数据。
强化学习
强化学习的输入数据作为对模型的反馈,强调如何基于环境而行动,以取得最大化的预期利益。
与监督式学习之间的区别在于,它并不需要出现正确的输入/输出对,也不需要精确校正次优化的行为。强化学习更加专注于在线规划,需要在探索(在未知的领域)和遵从(现有知识)之间找到平衡。
例:学习下围棋、打星际争霸、DotA2、双人德州扑克。(全部都是1v1的场景,目前强化学习领域对于多人博弈研究的很少)
特点:决策流程,激励系统,学习一系列的行动。
迁移学习
迁移学习是通过从已学习的相关任务中迁移其知识来对需要学习的新任务进行提高。
例:牛津的VGG模型、谷歌的Inception模型和word2vec模型、微软的ResNet模型。
特点:需求的训练数据集合较小、训练时间较小、可以方便的进行迁移以满足个性化。
机器学习的定义
对于某类任务T和性能度量P,一个计算机程序被认为可以从经验E中学习是指,通过经验E改进后,它在任务T上由性能度量P衡量的性能有所提升。
- 任务T:分类,翻译等机器学习的目标任务
- 性能度量P:准确率
- 经验E:训练集
欠拟合和过拟合
欠拟合:模型拟合不够,在训练集上拟合情况很差。往往会出现偏差大、方差小的情况;
过拟合:模型过度拟合,在训练集上拟合情况很好,但是在测试集上拟合情况很差。往往会出现偏差小、方差大的情况。
机器学习中,出现欠拟合时,解决办法有:
- 增加新特征,可以考虑加入特征组合、高次特征,来增大假设空间;
- 尝试非线性模型,比如核SVM 、决策树、DNN等模型;
- 如果有正则项可以减小正则项参数λ;
- Boosting,Boosting 往往会有较小的 Bias,比如 Gradient Boosting 等。
深度学习中,出现欠拟合时,解决办法有:
- 选择合适的损失函数;
- 尝试采用Mini-batch以及Batch Norm的方法进行优化;
- 选用其他激活函数;
- 采用自适应学习率的优化算法;
- 进行优化时考虑Momentum。
机器学习中,出现过拟合时,解决办法有:
- 交叉检验,通过交叉检验得到较优的模型参数;
- 特征选择,减少特征数或使用较少的特征组合,对于按区间离散化的特征,增大划分的区间;
- 正则化,常用的有 L1、L2 正则。而且 L1正则还可以自动进行特征选择;
- 如果有正则项则可以考虑增大正则项参数λ;
- 增加训练数据有限程度上可以避免过拟合;
- Bagging,将多个弱学习器Bagging 一下效果会好很多,比如随机森林等。
深度学习中,出现过拟合时,解决办法有:
- 早停,训练时可以每过n个Epoch就在验证集上检查误差,如果发现验证误差不降反增就可以停止训练了;
- 正则化,和机器学习一样,在深度学习中使用正则化完成权值衰减可以防止过拟合;
- Dropout,Dropout也是一种正则化手段,指暂时丢弃一部分神经元及其连接。随机丢弃神经元可以防止过拟合,同时可以高效地连接不同网络架构。
误差来源分析
偏差bias
期望预测与真实标记的误差,偏差越大偏离理论值越大。
在一个训练集\(D\)上模型\(f\)对测试样本\(x\)预测输出为\(f(x;D)\), 那么学习算法\(f\)对测试样本\(x\)的期望预测为: \[ \bar{f}(x)=E_D[f(x;D)] \] 这里用偏差的平方来表示偏差的计算公式: \[ Bias^2(x)=(\bar{f}(x)-\hat{y})^2 \]
方差variance
预测模型的离散程度,方差越大离散程度越大。使用样本数相同的不同训练集产生的方差为: \[ var(x)=E_D[(f(x;D)-\bar{f}(x))^2 \]
噪声noise
真实标记与数据集中的实际标记间的偏差(\(y_D\)表示在数据集中的标记,\(\hat{y}\)表示真实标记,这两个可能不等):
\[ \epsilon=E_D[(y_D-\hat{y})^2] \]
泛化误差
学习器在新样本上的误差称为“泛化误差”。可以分解为三个部分: 偏差(bias), 方差(variance) 和噪声(noise).
以回归任务为例, 学习算法的平方预测误差期望为:
\[ Err(x)=E_D[(y_D-f(x;D))^2] \]
对算法的期望泛化误差进行分解,就会发现:泛化误差=偏差的平方+方差+噪声:
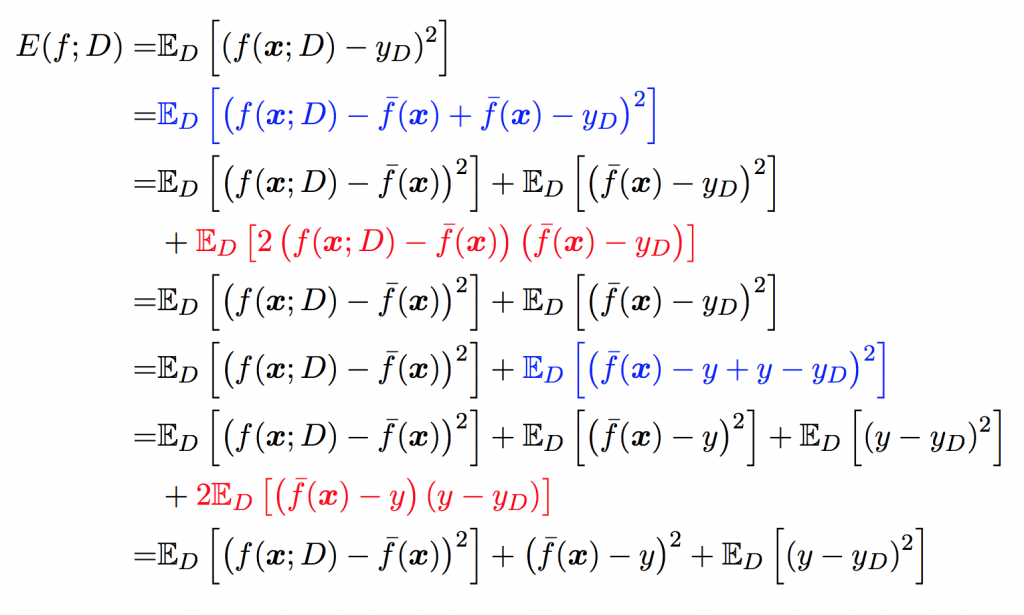
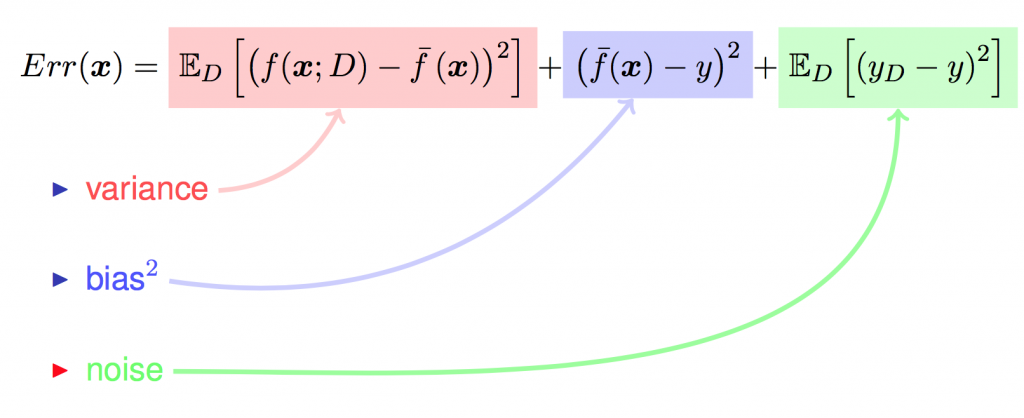
三类数据集
- 训练集:用于学习参数
- 开发/验证集:用于挑选超参数
- 测试集:用于估计泛化误差
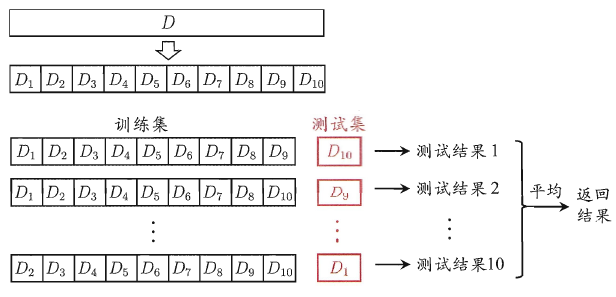
Cross Validation – 交叉验证
将数据集D划分成k个大小相似的互斥子集,每次用k-1个子集作为训练集,余下的子集做测试集,最终返回k个训练结果的平均值。交叉验证法评估结果的稳定性和保真性很大程度上取决于k的取值。适用于数据集不是特别大时。
参数 v.s. 超参数
模型参数是模型内部的配置变量,通过学习算法进行优化。例:神经网络中,层与层之间的权值W与偏置b。
超参数是一个学习算法的参数。它是不会被学习算法本身影响的,它优于训练,在训练中是保持不变的。例:学习率\(\eta\),正则系数\(\lambda\),模型阶数,模型类型,batch_size等。
正则化
L1-norm: 向量元素绝对值之和,即:
\[ \left \| \theta \right \|_1=\sum_{i=1}^{n}\left | \theta_i \right | \]
\[ L'(\theta)=L(\theta)+\lambda\left \| \theta \right \|_1 \]
——LASSO model: Tibshirani,1996
L2-norm: 各个元素的平方和,即:
\[ \left \| \theta \right \|_2=\sum_{i=1}^{n}\theta_i^2 \]
\[ L'(\theta)=L(\theta)+\lambda\left \| \theta \right \|_2 \]
——Ridge model: Hoerl,1970
Elastic Net (L1+L2):
\[ L'(\theta)=L(\theta)+\lambda[\rho\left \| \theta \right \|_1+(1-\rho)\left \| \theta \right \|_2 ] \]
正则化的作用:
对模型进行降阶,缩小模型空间,以解决过拟合的问题。
如何加快模型的训练
特征缩放/标准化
Feature Scaling – 特征缩放/归一化
输入值减去样本中最小值,然后除以样本范围,这样会使得结果永远在0~1的范围内,所有特征参数差不多一个速度优化到最低点。式子如下:
\[ x'=\frac{x-min(x)}{max(x)-min(x)} \]
Mean Normalization – 均值归一化
输入值减去样本均值,然后除以样本范围。式子如下:
\[ x'=\frac{x-min(x)}{max(x)-min(x)} \]
zero-mean normalization - 0均值标准化
标准化:让输入的值减去样本平均数μ,再除以样本标准差σ。经过这样的处理,数据符合标准正态分布,即均值为0,标准差为1。
\[ {x}'=\frac{x-\mu}{\sigma} \]
梯度下降的变种
Gradient Descent – 梯度下降
如果需要找到一个函数的局部极小值,必须朝着函数上当前点所对应梯度(或者是近似梯度)的反方向,前进规定步长的距离进行迭代搜索。
\[ w' \leftarrow w - \eta \frac{\partial L(w,b)}{\partial w} \]
\[ b' \leftarrow b - \eta \frac{\partial L(w,b)}{\partial b} \]
为什么要以梯度的反方向为更新方向?
因为梯度方向是函数方向导数最大的方向,所以沿着梯度方向的反方向更新的话,函数下降的变化率最大。
Stochastic Gradient Descent – 随机梯度下降
随机梯度下降的损失函数(使用MSE作为损失函数):
\[ L^{(i)}(w,b) = \frac{1}{2}(h_{w,b}(x^{(i)}) - \hat{y}^{(i)})^2 \]
通过公式可以看到,随机梯度下降每次更新只用到了一个样本,如果这个训练集有m个样本,那么梯度下降更新一次参数,随机梯度下降已经更新了m次参数了。
随机梯度下降的好处是:随机梯度下降的更新速度更快;
随机梯度下降所带来的坏处是:随机梯度下降的更新只参考了一个样本,所以更新时候的抖动现象很明显。
Mini-batch Gradient Descent – Mini-batch梯度下降
Mini-batch梯度下降是梯度下降和随机梯度下降的中和版本,Mini-batch梯度下降每次更新所考虑的样本是可以被指定的,如果总共有m个样本,那就可以在1~m中任意指定。
如果每次更新时所参考的样本数合适,那么既兼顾了随机梯度下降更新速度快的特性,又兼顾了梯度下降更新的稳定性。
调整学习率
当我们在训练过程中,发现loss下降的很慢时,可以适当增大学习率;发现loss不降反增的时候,要降低学习率。
Adagrad
Adagrad算法的学习率会根据迭代次数来放缓学习率,从而达到学习率越来越小的目的。通过公式可以看到,学习率是会一直除以前面所有梯度的平方和再开根号的,这一定是一个大于0的数,所以学习率会越来越小。但是防止一开始的时候梯度就是0,如果让分母变为0会导致错误的,所以后面还要跟一个很小的正数\(\epsilon\),最终的式子是这样的:
\[ w^{t+1} \leftarrow w^t - \frac{\eta}{\sqrt{\sum_{i=0}^{t}(g^i)^2+\epsilon}}g^t \]
Adagrad算法也有很多不足:
- 如果初始的学习率设置过大的话,这个学习率要除以一个较大梯度,那么此算法会对梯度的调节太大;
- 在训练的中后期,分母上梯度平方的累加将会越来越大,使\(gradient\to0\),使得训练提前结束。
RMSprop
Adagrad算法的改进版RMSprop算法:
\[ w^{t+1} \leftarrow w^t - \frac{\eta}{\sigma^t}g^t \qquad \sigma^t = \sqrt{\alpha(\sigma^{t-1})^2 + (1-\alpha)(g^t)^2} \]
Adagrad和RMSprop算法这两个算法很相近,不同之处在于RMSprop算法增加了一个衰减系数α来控制历史信息的获取多少。
SGD with Momentum (SGD-M)
SGD 在遇到沟壑时容易出现抖动现象。为此,可以为其引入动量 Momentum,加速 SGD 在正确方向的下降并抑制震荡。
\[ m_t \leftarrow \gamma m_{t-1} +\eta g^t \qquad w^t \leftarrow w^{t-1} - m_t \]
这里多了一个\(m_t\),可以将其想象为动量或者惯性,意味着参数更新方向不仅由当前的梯度决定,也与此前累积的下降方向有关。如果上一次梯度和只一次同方向,\(m_t\)会越来越大,参数也会更新越来越快;如果方向不同,\(m_t\)会比上次更小,参数更新速度减慢。\(\gamma\)是取上一次更新的动量大小,通常取 0.9 左右。
这使得参数中那些梯度方向变化不大的维度可以加速更新,并减少梯度方向变化较大的维度上的更新幅度。由此产生了加速收敛和减小震荡的效果。
SGD with Nesterov(NAG)
\[ g^t\leftarrow \frac{\partial L(w^t- \gamma m_{t-1})}{\partial w} \qquad m_t \leftarrow \gamma m_{t-1} +\eta g^t \qquad w^t \leftarrow w^{t-1}-m_t \]
NAG算法在SGD-M上进一步改进,计算\(g^t\)时有所不同。简单解释来说就是,在SGD-M算法中,更新参数要用到上一次更新的动量;换句话说,下一次更新也会用到这一次更新的动量。那么可以通过这一次更新的动量大概预估出下一次把参数更新到哪里,然后提前去那个地方看看梯度,如果梯度方向改变很小,那么就知道下一次更新和这一次更新方向差不多,是朝着最低点前进,那么步子就可以迈大一点;如果梯度方向改变很大,那么就知道下一次更新在不断震荡的过程中,那么步子迈小一点,减小震荡幅度。
这个解释很不严谨,上面的式子可以转换为二阶导的形式,也就是每次更新,要看上一次更新的动量,当前点的梯度值,还有一个二阶导数。有兴趣看看这个文章一起愉快的推公式吧~
分类问题
如何区分回归问题与分类问题
输出值可以有限枚举出来就是分类问题,否则就是回归问题。
为什么不可以用线性回归的模型解决分类问题
多分类问题中,如果使用线性回归模型,按输出值进行分类,那么就必须人为划分分类区间,使得有些分类距离很近,有些分类距离很远,极大影响了分类器性能。
在Logistic Regression中,为何使用Cross Entropy作为损失函数而不使用MSE
Logistic Regression的假设函数如下:
\[ \sigma(z) = \frac{1}{1+e^{-z}} \quad z(x) = wx+b \]
σ(z)分别对w和b求导,结果为:
\[ \frac{\partial \sigma(z)}{\partial w} = \frac{\mathrm{d} \sigma(z)}{\mathrm{d} z} \frac{\partial z}{\partial w}= \sigma(z)(1-\sigma(z))\times x \]
\[ \frac{\partial \sigma(z)}{\partial b} = \frac{\mathrm{d} \sigma(z)}{\mathrm{d} z} \frac{\partial z}{\partial b}= \sigma(z)(1-\sigma(z)) \]
如果使用MSE作为损失函数的话,那写出来是这样的:
\[ L(w,b) = \frac{1}{2m}\sum_{i=1}^{m}(\sigma_{w,b}(x^{(i)}) - \hat{y}^{(i)})^2 \]
当我们使用梯度下降来进行凸优化的时候,分别需要计算L(w,b)对w和b的偏导数:
\[ \frac{\partial L(w,b)}{\partial w} = \frac{1}{m}\sum_{i=1}^{m}(\sigma_{w,b}(x^{(i)}) - \hat{y}^{(i)})\sigma_{w,b}(x^{(i)})(1-\sigma_{w,b}(x^{(i)}))x^{(i)} \]
\[ \frac{\partial L(w,b)}{\partial b} = \frac{1}{m}\sum_{i=1}^{m}(\sigma_{w,b}(x^{(i)}) - \hat{y}^{(i)})\sigma_{w,b}(x^{(i)})(1-\sigma_{w,b}(x^{(i)})) \]
所以在σ(x)接近于1或者0的时候,也就是预测的结果和真实结果很相近或者很不相近的时候,σ(x)和1-σ(x)中总有一个会特别小,这样会导致梯度很小,从而使得优化速度大大减缓。
而当使用Cross Entropy作为损失函数时,损失函数为:
\[ L(w,b) = \frac{1}{m}\sum_{i=1}^{m}(-\hat{y}^{(i)}\log(\sigma_{w,b}(x^{(i)})) - (1-\hat{y}^{(i)})\log(1-\sigma_{w,b}(x^{(i)}))) \]
\(L(w,b)\)分别对\(w\)和\(b\)求偏导,结果如下:
\[ \frac{\partial L(w,b) }{\partial w}= \frac{1}{m}\sum_{i=1}^{m}(\sigma_{w,b}(x^{(i)})-\hat{y}^{(i)})x^{(i)} \]
\[ \frac{\partial L(w,b) }{\partial b}= \frac{1}{m}\sum_{i=1}^{m}(\sigma_{w,b}(x^{(i)})-\hat{y}^{(i)}) \]
这样梯度始终和预测值与真实值之差挂钩,预测值与真实值偏离很大时,梯度也会很大,偏离很小时,梯度会很小。所以我们更倾向于使用Cross Entropy而不使用MSE。
级联逻辑回归(Cascading logistic regression model)模型是啥?为什么要引入这个概念?
级联逻辑回归模型是将很多的逻辑回归接到一起,以进行特征转换再用一个逻辑回归来进行分类。
级联逻辑回归模型是神经网络的雏形。
Loss Function – 损失函数
回归任务假设函数:
\[ h_{w,b}(x) = wx+b \]
分类任务假设函数:
\[ h_{w,b}(x) = \sigma(wx+b) \]
在回归任务中,多使用均方误差作为损失函数:
\[ L(w,b) = \frac{1}{2m}\sum_{i=1}^{m}(h_{w,b}(x^{(i)}) - \hat{y}^{(i)})^2 \]
在分类任务中,多使用交叉熵作为损失函数:
\[ L(w,b) = \frac{1}{m}\sum_{i=1}^{m}[-\hat{y}^{(i)}\ln(h_{w,b}(x^{(i)})) - (1-\hat{y}^{(i)})\ln(1-h_{w,b}(x^{(i)}))] \]
Sigmoid和Softmax
Sigmoid Function不具体表示哪一个函数,而是表示一类S型函数,常用的有逻辑函数σ(z): \[ \sigma(z) = \frac{1}{1+e^{-z}} \]
Softmax,或称归一化指数函数,是逻辑函数的一种推广,二分类情况下,Softmax退化为逻辑函数。该函数的形式通常按下面的式子给出:
\[ \sigma(z)_{j} = \frac{e^{z_{j}}}{\sum_{k=1}^{K}e^{z_{k}}} \quad j = 1,...,K \]
Deep Learning
Deep Learning三步曲
- 定义一个Model,深度学习里Model是Neural Network Structure;
- 定义这个Model好坏,使用合适的Loss Function来衡量损失;
- 找出最佳参数,使用反向传播不断优化参数,从而找出最佳参数。
梯度不稳定问题
根本原因在于靠近输入层的梯度是来自于靠近输出层上梯度的乘积。当存在过多的层次时,就出现了内在本质上的不稳定场景。
Vanishing Gradient Problem - 梯度消失问题
在多层网络中,影响梯度大小的因素主要有两个:权重和激活函数的偏导。深层的梯度是多个激活函数偏导乘积的形式来计算,如果这些激活函数的偏导比较小(小于1)或者为0,那么梯度随时间很容易vanishing。
反向传播时,需要计算偏导数,如果激活函数是Sigmoid函数,对其求导后,发现Sigmoid函数的导数最大也就0.25(当input=0时),而且很多情况input不会为0的,所以Sigmoid的导数会更小。那么计算靠近输入层参数的偏导数,难免会乘上几次Sigmoid函数的偏导,梯度就这样消失了。
Exploding Gradient Problem - 梯度爆炸问题
和梯度消失一样,如果这些激活函数的偏导比较大(大于1),那么梯度很有可能就会exploding。这些大于1的偏导会导致靠近输入层的参数变化比较快,靠近输出层的参数相较而言变化慢,导致梯度爆炸的问题。
解决办法:
- 重新设计网络模型,减少网络层数有效解决梯度不稳定问题;
- 使用 ReLU 激活函数,ReLU求完微分后不会引起梯度消失或爆炸的问题,而且计算速度快,加速了网络的训练;
- 使用LSTM,LSTM单元和相关的门类型神经元结构可以减少梯度消失问题;
- 使用梯度截断,自定一个阈值,梯度再大也不能超过这个阈值;
- Batch-Norm,Batch-Norm通过对每一层的输出规范为均值和方差一致的方法,消除了w带来的放大缩小的影响,进而解决梯度消失和爆炸的问题;
- 残差网络结构,残差可以很轻松的构建几百层,一千多层的网络而不用担心梯度消失过快的问题,原因就在于残差的捷径(shortcut)部分。
RNN梯度消失与梯度爆炸
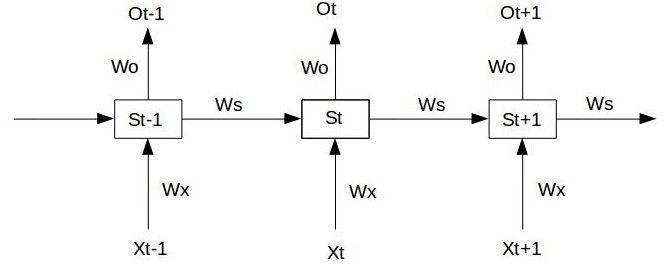
对RNN进行优化需要用到BPTT算法,使用\(S_i\)来表示RNN的记忆状态,权值\(W_x\)的偏导如下:
\[ \frac{\partial{L_{t}}}{\partial{W_{x}}}=\sum_{k=0}^{t}{\frac{\partial{L_{t}}}{\partial{O_{t}}}\frac{\partial{O_{t}}}{\partial{S_{t}}}}(\prod_{j=k+1}^{t}{\frac{\partial{S_{j}}}{\partial{S_{j-1}}}})\frac{\partial{S_{k}}}{\partial{W_{x}}} \]
发现其中\(\prod_{j=k+1}^{t}{\frac{\partial{S_{j}}}{\partial{S_{j-1}}}}\)是一个累乘,如果每一项都小于1,那么乘多了就变0了,如果每一项都大于1,那么乘多了又会很大,所以RNN存在梯度消失和爆炸的原因。
为什么LSTM可以解决梯度消失的问题
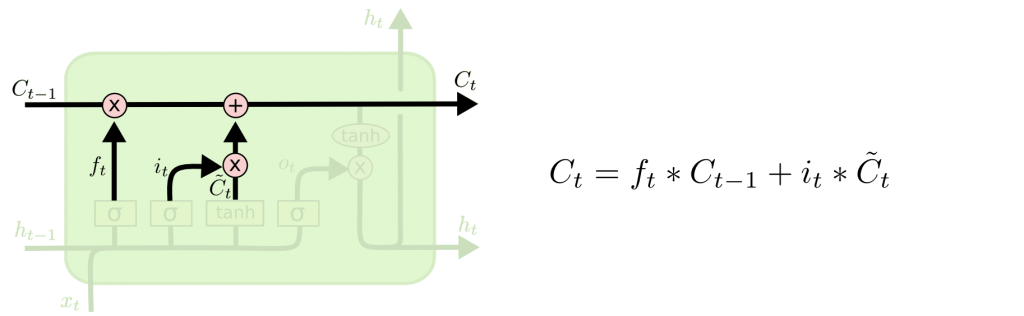
在LSTM中,也有和RNN一样的记忆部分,叫做细胞状态(LSTMCell),用\(C_i\)来表示。从上图可以看到,LSTM的单元状态\(C_i\)更新公式如图右侧所示,是一个加法而不是乘法,\(f_t\times C_{t-1}\)表示以前的记忆需要忘记多少;\(i_t\times \tilde{C}_t\)表示这一次的输入需要添加多少。因为是加法,所以不容易导致\(C_i\)接近于0的情况。
Maxout Function
Maxout Function可以理解成一种分段线性函数来近似任意凸函数,因为任意的凸函数都可由分段线性函数来拟合。它在每处都是局部线性的,而一般的激活函数都有明显的曲率。ReLU是Maxout的一种特殊情况。
Dropout
Dropout也是一种正则化手段,指暂时丢弃一部分神经元及其连接。随机丢弃神经元可以防止过拟合,同时可以高效地连接不同网络架构。
如果训练时有p%的概率dropout,那么在测试的时候,所有的权值都要乘以1-p%。
举个栗子:如果训练时有30%的概率dropout,那么在测试的时候,所有的权值都要乘以0.7。如果其中一个权重为10,则要乘以0.7,权值为7。
Convolutional Neural Network
CNN和RNN内容这么多我要写啥???
当输入为图像时使用CNN,CNN会自动学习到图像特征。
与全连接神经网络不同之处:
- CNN采取稀疏连接的方式;
- 权值共享,一个卷积核可以对一张图片很多像素值进行操作。
CNN特点:
- 一些pattern只和图片局部区域有关;
- 图片的不同区域可能会出现的同样的pattern;
- 对图片进行降采样处理并不会改变图片的内容。
卷积层用到1、2两个特点,池化层用到3特点。
CNN里的超参数:
- Filter Size - 卷积核的尺寸
- Padding - 边缘填充策略(不知道这个怎么翻才好)
- Stride - 移动步长
- number of filters - 卷积核的个数
Recurrent Neural Network
什么是序列数据?会举例说明。
有时间维度的数据称为序列数据。例:音乐,语音。
即使只有一层的RNN模型,仍可能出现梯度消失和梯度爆炸,为什么?
见上面的RNN梯度消失与梯度爆炸部分。
LSTM与一般的RNN相比,优势在哪?
- 见上面为什么LSTM可以解决梯度消失的问题。
- LSTM可以保持长时记忆,LSTM的记忆门可以控制记忆存放多久。不过LSTM可以保持长时间记忆根本原因也是因为LSTM解决了梯度消失的问题吧。
对于给定问题,能判断出是否该使用RNN模型。
当输入和输出有一个是序列数据时使用RNN模型。
References:
https://zhuanlan.zhihu.com/p/26304729
https://feisky.xyz/machine-learning
https://blog.csdn.net/fjssharpsword/article/details/71157798
https://www.jianshu.com/p/b8844a62b04a
https://zhuanlan.zhihu.com/p/32626442
https://zhuanlan.zhihu.com/p/22810533
https://cloud.tencent.com/developer/article/1013598
https://ziyubiti.github.io/2016/11/06/gradvanish/
