算法知识梳理
简单梳理一下算法知识,主要面向需要找工作的同学,希望能对你们笔试有所帮助。
从原理到代码(我是一个全凭学生自己领悟的老师🌚)
练习题 - 最少次数
时间复杂度
时间复杂度是什么
时间复杂度描述的是这个算法的运行时间。
如何计算时间复杂度
计算语句的运行次数
例:插入排序算法 Insert-sort(A)
1 | for j from 2 to length[A] |
| 代码行数 | 语句执行时间 | 执行次数 |
|---|---|---|
| 1 | \(C_1\) | \(n\) |
| 2 | \(C_2\) | \(n-1\) |
| 3 | \(C_3\) | \(n-1\) |
| 4 | \(C_4\) | \(\sum_{j=2}^{n}t_j\) |
| 5 | \(C_5\) | \(\sum_{j=2}^{n}(t_j-1)\) |
| 6 | \(C_6\) | \(\sum_{j=2}^{n}(t_j-1)\) |
| 7 | \(C_7\) | \(n-1\) |
- 其中\(t_j\)表示第\(j\)次循环while语句执行的次数
总运行代价 \[ T(n)=C_1n+C_2(n-1)+C_3(n-1)+C_4\sum_{j=2}^{n}t_j+C_5\sum_{j=2}^{n}(t_j-1)+C_6\sum_{j=2}^{n}(t_j-1)+C_7(n-1) \] 最好情况:输入数据状态为升序,此时\(A[i]≤key\),所以\(t_j=1\)
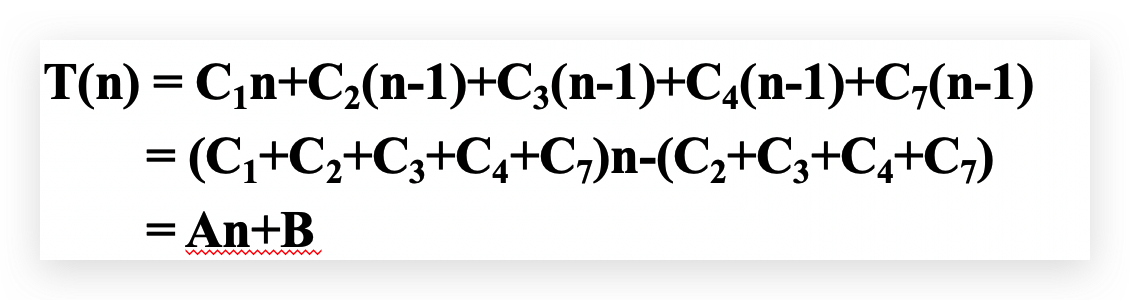
最坏情况:输入数据状态为倒序,此时\(A[i]>key\),所以\(t_j=j\)
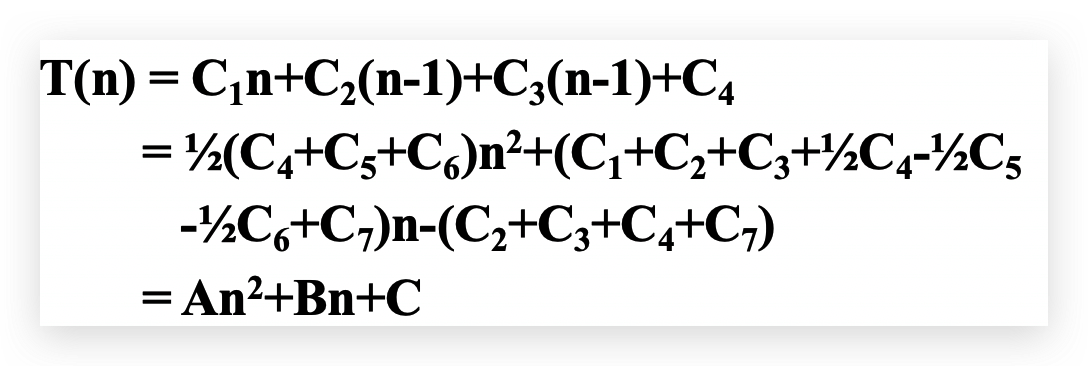
平均情况:是指在不同的输入条件下算法平均的运行时间。插入A[j]时需比较\(\frac{j}{2}\)次,即\(t_j=\frac{j}{2}\)所以T(n)应和\(n^2\)相关。
对于三种情况下算法的时间复杂度,通常会更多地关注最坏情况下的时间复杂度,原因为:
- 是算法运行时间的上限,也是算法改进的一个判断标准
- 在很多时间问题中,由于缺少足够的信息,因此算法往往运行在最坏请况
- 算法的平均情况下的时间往往与最坏情况下的时间复杂度相同
渐进符号
定义:
\(f(n)\)是一个算法的语句执行次数,将上面的C1C2...都取1即可。
\(\Theta(g(n))=f(n)\)
存在大于0的常数\(C_1\)、\(C_2\)和\(n_0\),使得对于所有的\(n \geq n_0\),都有\(0\leq C_1g(n) \leq f(n) \leq C_2g(n)\),记为\(f(n)=\Theta(g(n))\)。
\(O(g(n))=f(n)\)
存在大于0的常数C、\(n_0\),使得对于所有的\(n \geq n_0\),都有\(0 \leq f(n) \leq Cg(n)\),记为\(f(n)=O(g(n))\)。
\(\Omega(g(n))=f(n)\)
存在正常数C和\(n_0\),使得对于所有的\(n \geq n_0\),都有\(0 \leq Cg(n) \leq f(n)\),记为:\(f(n)=\Omega(g(n))\)
三个符号间的关系
对于任意的函数f(n)和g(n),当且仅当\(f(n)=O(g(n))\)且\(f(n)=Ω(g(n))\)时,\(f(n)=Θ(g(n))\)。
一些已知量间的渐进关系
\[ \lim_{n\rightarrow \infty}\frac{f(n)}{g(n)}=\left\{\begin{matrix} 0 & \Rightarrow f(n)<g(n)\Rightarrow & f(n)=O(g(n))\\ C & \Rightarrow f(n)=g(n)\Rightarrow & f(n)=\Theta(g(n))\\ \infty & \Rightarrow f(n)>g(n)\Rightarrow & f(n)=\Omega(g(n))\\ \end{matrix}\right. \]
最坏情况下: \[ f(n)=\frac{3}{2}n^2+\frac{13}{2}n-6 \] 证明:
存在大于0的常数8,使得对于所有的\(n \geq 1\)时, \[ f(n)=\frac{3}{2}n^2+\frac{13}{2}n-6 \leq 8n^2=\frac{3}{2}n^2+\frac{13}{2}n^2 \] 所以证明得\(f(n)=O(n^2)\)
如果不需要严格证明,那么直接分析语句的执行次数,最高项的数量级就是他的时间复杂度。
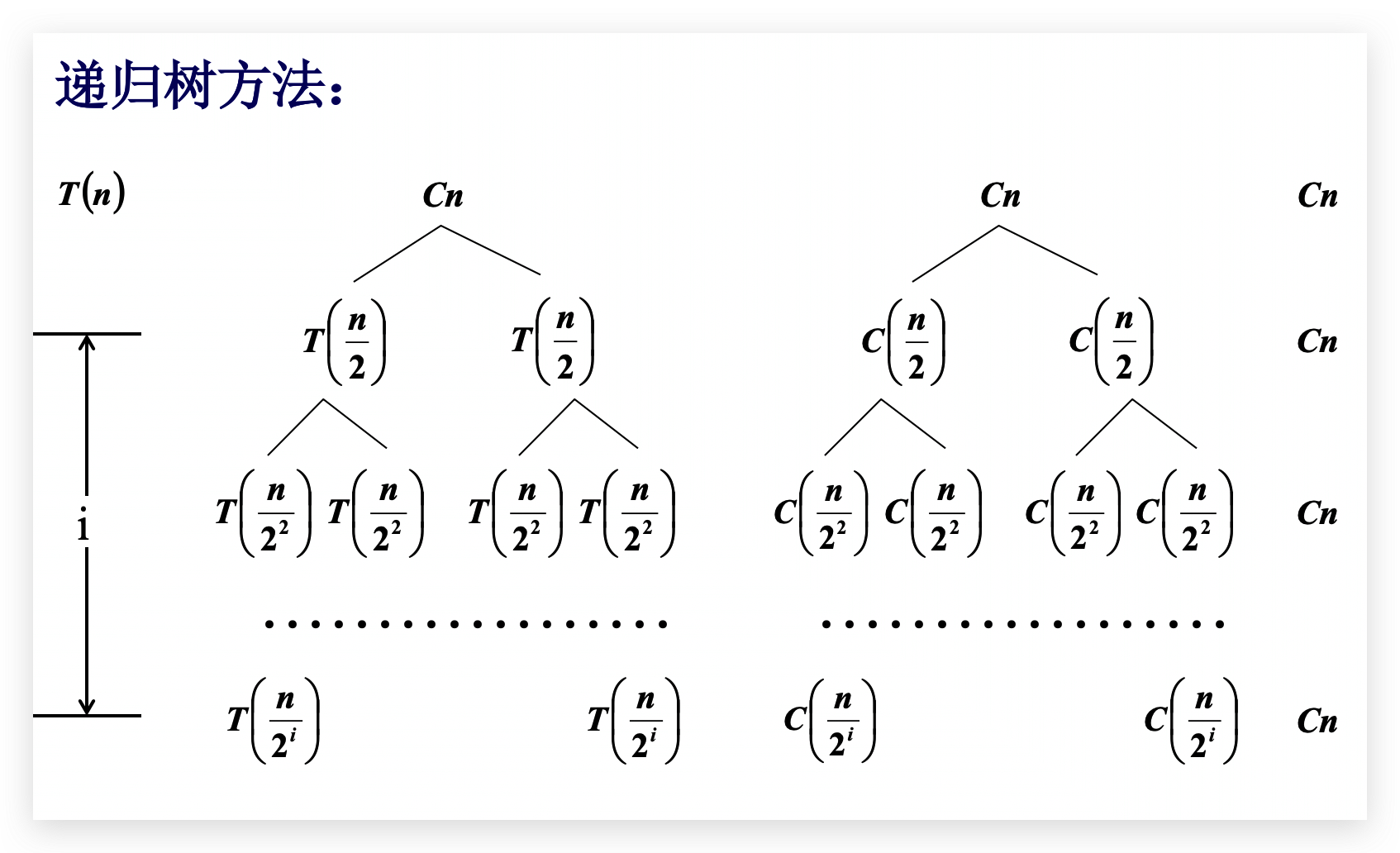
如果是递归算法:
递归树法:分析出递归树的树高以及树的每一层所耗时间,树高\(\times\)每一层的时间就是总耗时,一般带有\(O(\log n)\)
*Master方法 \[ T(n)=aT(\frac{n}{b})+f(n) \] 其中a≥1,b>1且为常数,f(n)为渐进函数:
Case1: \(f(n) = O(n^{\log_{b}{a-\epsilon}})\),常数\(\epsilon>0\),
则\(T(n)=\Theta(n^{\log_{b}{a}})\)
Case2: \(f(n) = \Theta(n^{\log_{b}{a}})\),
则\(T(n)=\Theta(n^{\log_{b}{a}}\lg n)\)
Case3: \(f(n) = \Omega(n^{\log_{b}{a+\epsilon}})\),常数\(\epsilon>0\),且满足\(af(\frac{n}{b}) \leq cf(n)\),\(c<1\)且n足够大,
则\(T(n)=\Theta(f(n))\)
Case4: \(f(n) = \Omega(n^{\log_{b}{a}}\lg^kn)\),其中\(k \geq 0\),
则\(T(n) = \Theta(n^{\log_{b}{a}}\lg^{k+1}n)\)
常见的时间复杂度:
- \(O(1)\): 表示算法的运行时间为常量
- \(O(n)\): 表示该算法是线性算法
- \(O(\log n)\): 二分查找算法
- \(O(n^2)\): 对数组进行排序的各种简单算法,例如直接插入排序的算法。
- \(O(n^3)\): 做两个n阶矩阵的乘法运算
- \(O(2^n):\) 求具有n个元素集合的所有子集的算法
- \(O(n!)\): 求具有N个元素的全排列的算法
分治法
什么是分治法
当求解的问题较复杂或规模较大时,不能立刻得到原问题的解。
但这些问题本身具有这样的特点:
- 它可以分解为若干个与原问题性质相类似的子问题
- 这些子问题较简单可方便得到它们的解
- 可以通过合并这些子问题的解就可得到原问题的解
使用分治法的步骤:
- 分解问题(divide):把原问题分解为若干个与原问题性质相类似的子问题
- 求解子问题(conquer):不断分解子问题直到可方便求出子问题的解为止
- 合并子问题的解(combine):合并子问题的解得到原问题的解
分治法适用条件
- 原问题可以分解为若干个与原问题性质相类似的子问题
- 问题的规模缩小到一定程度后可方便求出解
- 子问题的解可以合并得到原问题的解
- 分解出的各个子问题应相互独立,即不包含重叠子问题
分治法的时间复杂度计算
\[ T(n)=\left\{\begin{matrix} \Theta(1) & n \leq C\\ aT(\frac{n}{b})+D(n)+C(n) & n > C\\ \end{matrix}\right. \]

举个栗子
归并排序(Merge Sort)
直接对所有数据进行排序是很复杂的一个问题,但是如果只对一小部分的数据进行排序,那么问题的会变得简单一些。
比如有十万个数据要排序,我们很难解决这个问题,但是如果只对10个数据进行排序,那是不是看一看就能解决了。
归并排序就是不断的减小问题的规模,直到可以方便排序了,那么就排序,再把排序好的结果整合起来。
什么时候方便排序了呢?如果不断减小数据量到1,长度为1的数组是不是一定有序的,那么此时子问题秒解,剩下要做的就是把已经解决的子问题合并起来。
应用分治法解题的三个基本步骤为:
- divide:把具有n个元素的数组分解为二个n/2大小的子数组
- conquer:递归地分解子数组,直到子数组只包含一个元素为止
- combine:二二合并已排好序的子数组使之成为一个新的排好序的子数组,重复这样二二合并的过程直到得到原问题的解
由分治法三个步骤可方便得到解此问题的算法:
Merge-sort函数
1 | Merge-sort(A,p,r) |
Merge函数:
1 | Merge(A,p,q,r) |
时间复杂度:

动态规划 - Dynamic Programming
前面铺垫了这么多,其实就是为了讲动态规划的。最近一个月看过几个同学的面试题,一半左右的题都在考动态规划,确实动态规划是一个比较适合笔试,又很实用的算法,而且想考的难会非常难,想考的容易,好像也不会多容易。
先来个很装逼的开场
Those who cannot remember the past are condemned to repeat.
-Dynamic Programming
大意是,不记过往之人,活该重蹈覆辙。
动态规划的主体思想就是,已经求过的问题,不再重复求解。把求得的解记在小本本上,下次再用时,直接读值即可。记得我们算法老师讲过,Dynamic Programming中的Programming不是编程的意思,就是不断的维护一个数组,求得一个值放进去,需要用时再取出来。
动态规划和分治法有类似之处,他们都是通过组合子问题的解来求解原问题。不同之处在于,分治法常常用于将原问题划分为几个互不相交的子问题,如果划分后,有很多完全相同的子问题,那就使用动态规划的思路比较好。这些完全相同的子问题只需要求解一次,然后把值保留下来,后面直接去读值即可。
设计动态规划算法的步骤
- 描述问题的最优解(optimal solution)结构特征
- 递归定义最优解值
- 自底向上计算最优解值
- 从已计算得到的最优解值信息中构造最优解
什么样的问题适合使用动态规划算法求解
最优子结构性质
最优子结构性质是应用动态规划方法的必要前提,即所解问题必须具有最优子结构性质才能用动态规划方法求解。
所谓最优子结构性质是指一个问题的最优解中所包含的所有子问题的解都是最优的。
这句话不太好理解,举个栗子:
现在有3个城市,分别为ABC,我必须要先从A到B,再从B到C,我的目标是使得路程耗时尽可能短。
假设 现在有一条A到C的路线是总耗时最短的,也就是最优解。
那么这条路线中,A到B的耗时一定也是最优解,B到C的耗时一定也是最优解。
假设此时总耗时3个小时,其中A到B耗时2小时,B到C耗时1小时。
反证:如果A到B的耗时不是最优解,那么就存在一个更优解,耗时更短,比如1小时,用这个最优解代替当前解,使得A到B的耗时变短了,那也也使得总耗时变短了,成了2小时,则与假设(这条路线是最优解)矛盾。
如果一个问题能找到他的最优子结构,就可以将大问题划分为小问题,分治求解。
重叠子问题
动态规划能加速就是因为存在重叠子问题,只需要求解一次即可,那么将大大加速算法效率。
例题:钢条切割问题
题目
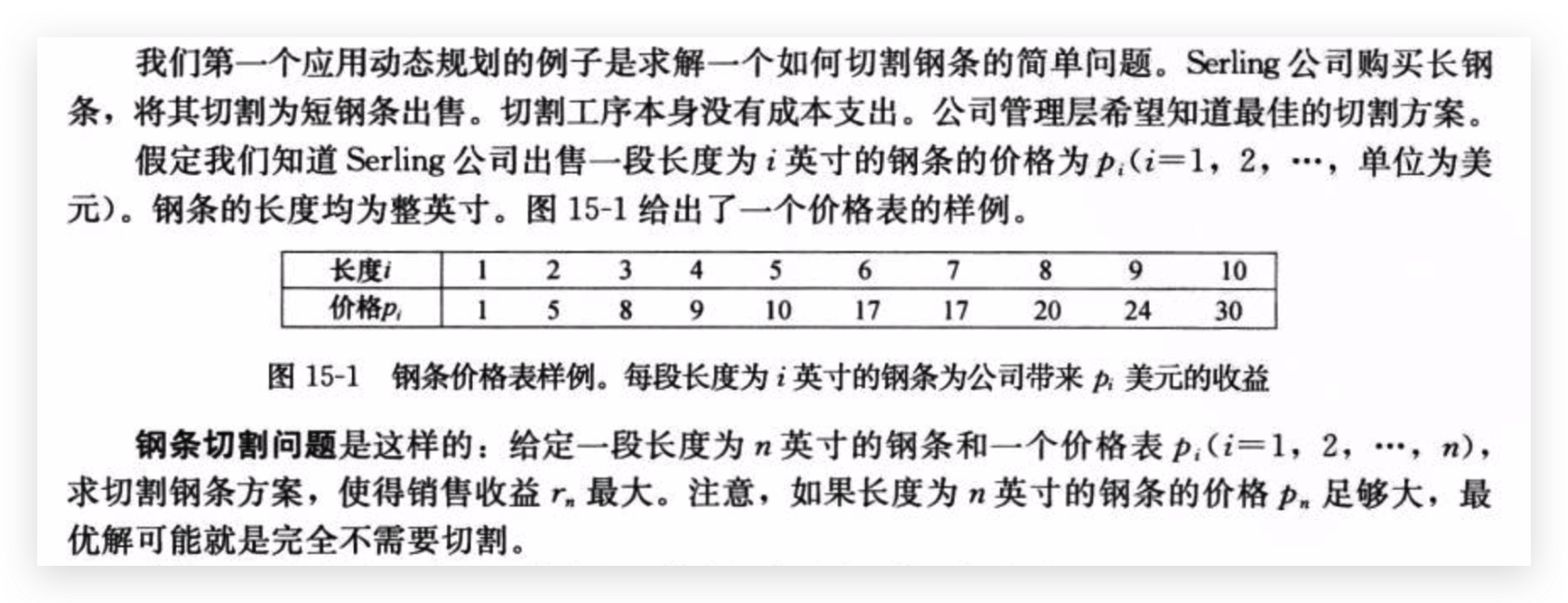
题目看懂了吗,没看懂我再解释一下:
现在有这么一张表(上图那个表格),表示每个长度的钢条能卖多少钱,但是发现这个价格不是线性的,长度为1的钢条1元/米,长度为10的钢条3元/米,长度6和长度7的钢条价钱甚至一样,那我如果有长度为7的钢条为何不切成长度为6和1的卖呢?长度为4的钢条,比起整个卖9元,我可以切成长度2和2,卖10元。
要求是,给定长度为n的钢条,问如何切割(当然也可以不切割),可以获得最大收益?
分析
使用最优子结构性质确定递推式
这是动态规划步骤第一步,描述问题的最优解(optimal solution)结构特征。
这个题目有很好的最优子结构性质,思考一下,现在有长度为n的钢条,如果我已经找到了最优的切割方案,把他切成了k段,那么就有: \[ n=i_1+i_2+...+i_k \] 这k段中的每一段一定也是受益最高的。
我觉得把逻辑正过来可能比较好理解:只有每一段都获取了最高的受益,那么总的受益才会最高。
还是一样的反证,如果有一段受益不是最高的,那么换种更高的受益方式,比如第三段长度为4,我是直接卖的,赚9块钱,除第三段的其他段赚了x元,那么总受益是9+x;但是我可以把第三段卖到10元(拆成2和2),那么总的可以卖10+x。
所以只有每一段都获取了最高受益,总受益才会最高。


钢条切割问题可以写出这样的递推式,这是动态规划步骤的第二步,递归定义最优解值: \[ r_{0n} = max_{0\leq i \leq \frac{n}{2}}(r_{0i} + r_{in}) \] 一个长度为n的钢条,从0~\(\frac{n}{2}\)找一个切割点,切成了两段,分别是\(0\to i\)为一段,记作\(r_{0i}\),\(i \to n\)为一段,记作\(r_{in}\),i的取值只需要从0取到\(\frac{n}{2}\)即可,因为再往后都是对称切割,比如把长度为5的切为1和4以及4和1,不需要重复考虑。
首先,不知道怎么切分才是最好的,所以切分点i要从0搜索到\(\frac{n}{2}\);
其次,每次切分完后,就对两个子钢条进行递归求解,即求子钢条的最大收益是多少,只有子钢条收益最高,组合起来收益才最高。
发现存在大量重叠子问题
比如我求长度为3的钢条,可以切分为:
- 0~3
- 1~2
比如我求长度为4的钢条,可以切分为:
- 0~4
- 1~3
- 2~2
发现都重复计算了长度为2的钢条最大收益,完全可以算完第一遍后,把结果存储起来,再用的时候,直接取结果就好。
求解
动态规划第三步,自底向上计算最优解值。
如果上面都没看懂,也没关系,看如何求解就明白了。
先把钢条价格表放在这里,好对应查找:

我们用下面的表来模拟动态规划算法,实际代码中,会有一个对应的数组来存储表中的数据。
首先表中元素都初始化为空,我们不知道最大收益是多少。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 |
长度为1的钢条最大收益是确定了,他又不能切分,除了卖掉只能丢掉,丢掉肯定不划算,卖掉还能赚俩钱,所以查表得,钢条长度为1时,最大收益为1。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 |
计算长度为2的钢条的最大收益,根据递推式: \[ r_{0n} = max_{0\leq i \leq \frac{n}{2}}(r_{0i} + r_{in}) \] 长度为2的钢条可以切分为:
- 0~2 收益为0+5=5
- 1~1 收益为1+1=2
显然不切割,直接卖长度为2的钢条收益最大。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 | 5 |
计算长度为3的钢条的最大收益,根据递推式: \[ r_{0n} = max_{0\leq i \leq \frac{n}{2}}(r_{0i} + r_{in}) \] 长度为3的钢条可以切分为:
- 0~3 收益为0+8=8
- 1~2 收益为1+5=6
显然不切割,直接卖长度为3的钢条收益最大。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 | 5 | 8 |
计算长度为4的钢条的最大收益,根据递推式: \[ r_{0n} = max_{0\leq i \leq \frac{n}{2}}(r_{0i} + r_{in}) \] 长度为2的钢条可以切分为:
- 0~4 收益为0+9=9
- 1~3 收益为1+8=9
- 2~2 收益为5+5=10
切割为2和2的长度钢条收益最大。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 | 5 | 8 | 10 |
计算长度为5的钢条的最大收益:
长度为5的钢条可以切分为:
- 0~5 收益为0+10=10
- 1~4 收益为1+10=11
- 2~3 收益为5+8=13
切割为2和2的长度钢条收益最大。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 | 5 | 8 | 10 | 13 |
计算长度为6的钢条的最大收益:
长度为6的钢条可以切分为:
- 0~6 收益为0+17=17
- 1~5 收益为1+13=14
- 2~4 收益为5+10=15
- 3~3 收益为8+8=16
不切割钢条收益最大。
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 | 5 | 8 | 10 | 13 | 17 |
依次类推,最后的表结果为
| 钢条长度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 最大收益 | 1 | 5 | 8 | 10 | 13 | 17 | 18 | 22 | 25 | 30 |
有没有发现这个过程中,之前算过的长度为234...最大收益被重复调用了,这就是动态规划加速的地方。
代码
1 |
|
练习1 - [编程|100分]硬币
1 | 时间限制:C/C++1秒,其他语言2秒 |
本题可使用本地IDE编码,不做跳出限制,编码后请点击“保存并调试”按钮进行代码提交。
题目描述
给定若干(不超过20种)不同面值的硬币和一个整数M (M<11000000)。求出可以组成M的最少硬币数。如果不存在任何一种组合得到M,输出-1。
输入描述
第一行为硬币面值,数字由逗号分开且逗号跟数字有任意空白字符。
第二行为整数M。
输出描述
一个整数,表示答案。
示例1
输入输出示例仅供调试,后台判题数据一般不包含示例。
输入
1 | 1, 2,5 |
输出
1 | 3 |
说明
用5+5+1的组和只需要3枚硬币就可以组成11。
题解
考虑最优子结构
首先考虑一下这一题满足怎样的最优子结构。
题目是要求组成价值M的最少硬币数,那么如果我将M切分为a和b,满足\(M=a+b\)
若M是用最少的硬币数组成,那么a和b一定也是用最少的硬币数组成。
正过来的逻辑是,只有a和b都用了最少的硬币数组成,那么M才会是使用了最少的硬币数组成。
递推式
用\(C_i\)表示:价值\(i\)至少需要\(C_i\)个硬币组成。
递推式有: \[ C_M = \min_{0 \leq i \leq \frac{M}{2}}(C_i+C_{M-i}) \] 这个递推式中,i是从0遍历到\(\frac{M}{2}\)
- i=0表示不切分M,即想用一张面值直接表示价值M;
- i>0表示把M切分为\(i\)和\(M-i\)两部分,分别求得\(C_i\)和\(C_{M-i}\),然后相加即为此次切分方案的最少硬币数。
可以发现这个递推式里,i是可以不用取0的,因为只有i刚好等于给定的面值,才可能被一张面值直接表示,当M不等于面值的价值时,是不可能被表示的,所以i只需要从1开始就好。
递推式改为: \[ C_M = \min_{1 \leq i \leq \frac{M}{2}}(C_i+C_{M-i}) \]
代码
1 |
|
例题:矩阵链乘法
题目
问题:给定一个矩阵序列<A1,A2,…,An>,其中矩阵Ai的维数为Pi-1×Pi,要求计算A1×A2×…×An矩阵链乘的先后顺序,使得总计算次数最少?
例:四个矩阵相乘A1×A2×A3×A4的链乘共有五种链乘顺序。

考虑这个问题有什么意义呢?不同的相乘顺序所造成的计算量是差别很大的,假设有三个矩阵A1×A2×A3,其中矩阵的维数为:10×100,100×5,5×50。
如果12两个矩阵先相乘,再和3相乘,那么总计算量=\(10 \times 100 \times 5 + 10 \times 5 \times 50 = 7500\)
但如果23两个矩阵先相乘,再和1相乘,那么总计算量=\(100\times 5\times 50+10\times 100 \times 50=75000\)
相差了有10倍的计算量。
讲课时写的板书
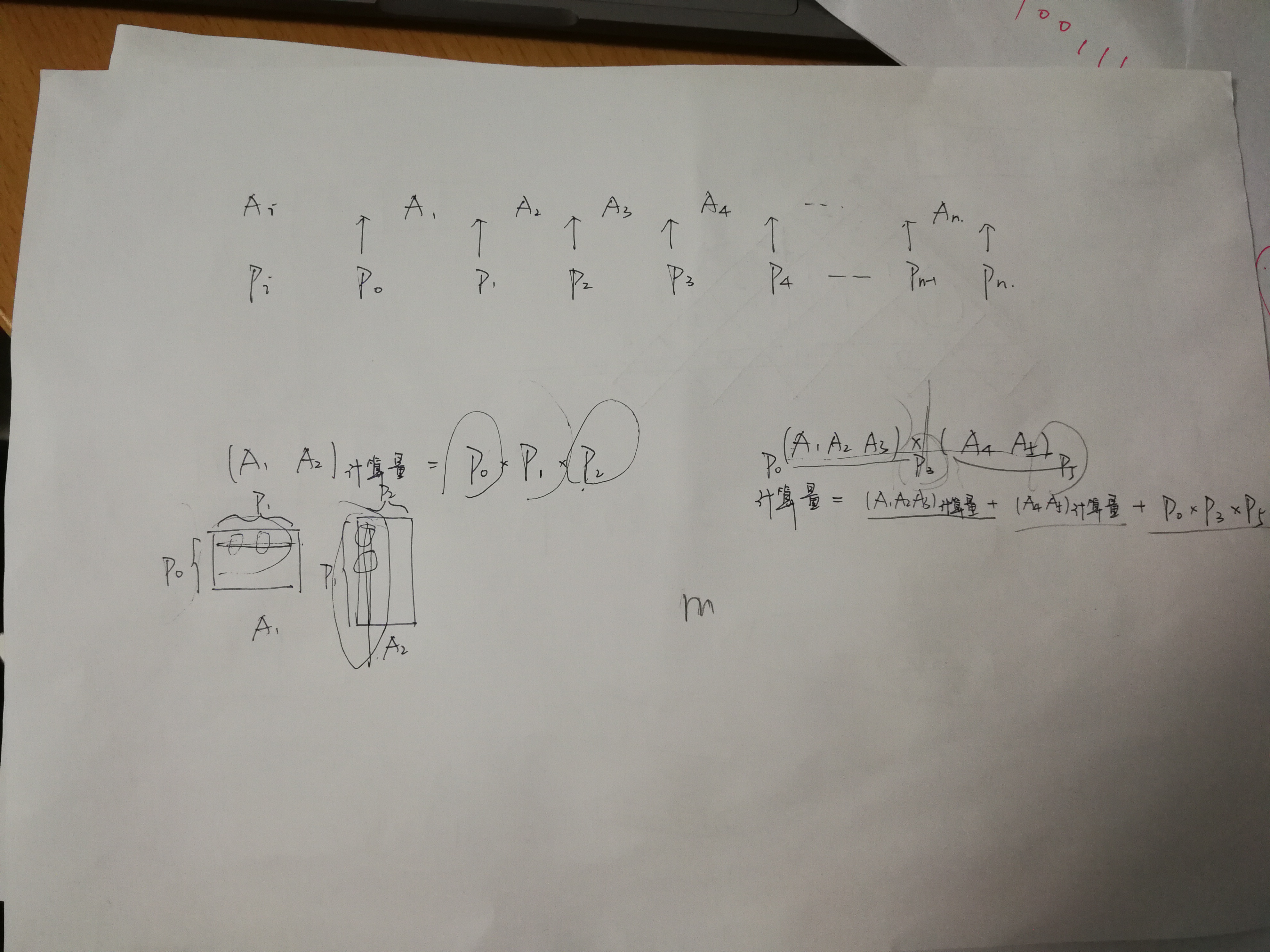
\(A_1A_2A_3...A_n\)是各个矩阵
\(p_0p_1p_2...p_n\)是每个矩阵的行数和列数
下面解释了如何计算两个矩阵相乘的计算量,以及如何计算矩阵链的计算量
分析
step1 思考问题最优子结构
若子问题\(A_{ij}\)的解\((A_iA_{i+1}…A_j)\)是一个最优解
则在\(A_{ij}\)中一定存在一个最佳分裂点\(k(i≤k<j)\),使得子链\(A_{ik}\)和\(A_{k+1j}\)的解,即\((A_iA_{i+1}…A_{k})\)和\((A_{k+1}…A_{j})\)也是最优的。
证明:
假设现在已知最佳分裂点k,那么矩阵链\((A_iA_{i+1}…A_j)\)可以写为\((A_iA_{i+1}…A_k) \times (A_{k+1}A_{k+2}…A_j)\)。
这里引入\(p\)数组,用以记录矩阵链中,每个矩阵的行和列,比如\(p_{i-1}\)记录了\(A_i\)的行数,\(p_{i}\)记录了\(A_i\)的列数,同时也是\(A_{i+1}\)的行数。
\((A_iA_{i+1}…A_k)\)的shape是\(p_{i-1} \times p_{k}\)
\((A_{k+1}A_{k+2}…A_j)\)的shape是\(p_{k} \times p_{j}\)
那么有:
矩阵链\((A_iA_{i+1}…A_j)\)的计算量 = 矩阵链\((A_iA_{i+1}…A_k)\)的计算量 + \((A_{k+1}A_{k+2}…A_j)\)的计算量 + \(p_{i-1}p_{k}p_{j}\)
从上面的式子可以看出最优子结构,如果等号左边的计算量最小,那么右边两个计算量也必须是最小的。
正过来的逻辑是,只有切分点左右两个矩阵链都把各自的计算量控制在最小,那么总计算量才能是最小的。
反证也很容易,和上面反证一个思路。
step2 由最优子结构写出递归式
用m这个二维矩阵定义计算量,\(m[i, j]\)表示矩阵链\((A_iA_{i+1}…A_j)\)的计算量。
有递推式: \[ m[i, j]=\left\{\begin{matrix} 0 & \text{if i = j}\\ min_{i \leq k < j}(m[i, k] + m[k+1, j] + p_{i-1}p_{k}p_{j}) & \text{if i < j}\\ \end{matrix}\right. \] 解释一下:
- 如果i=j,那么就说明矩阵链中只有一个矩阵,一个矩阵有啥计算量,取值为0;
- 如果i<j,那么矩阵链中多于一个矩阵,这时候就要找切分点k了,我们不知道从哪里切分是最好的,所以只能是挨个遍历,从i遍历到j,将每种可能的情况都计算一下计算量,取最小的计算量,作为此矩阵链的计算量。
step3 自底向上求解
同样是开数组记录下数值,但是这次是二维数组,我不想挨个画图了,详细讲一下下面这个三角形吧。
我们可以看到左边这个三角形有两个index,左边的index是j,右边的index是i,表示这个矩阵链从i到j的子链,最少计算量是多少。
右边那个三角形表示此时的k取值,也就是切分点在哪,三角形同样也是两个index,但是右边比左边少1行,因为左边最下面一行表示单个矩阵,没有切分点。

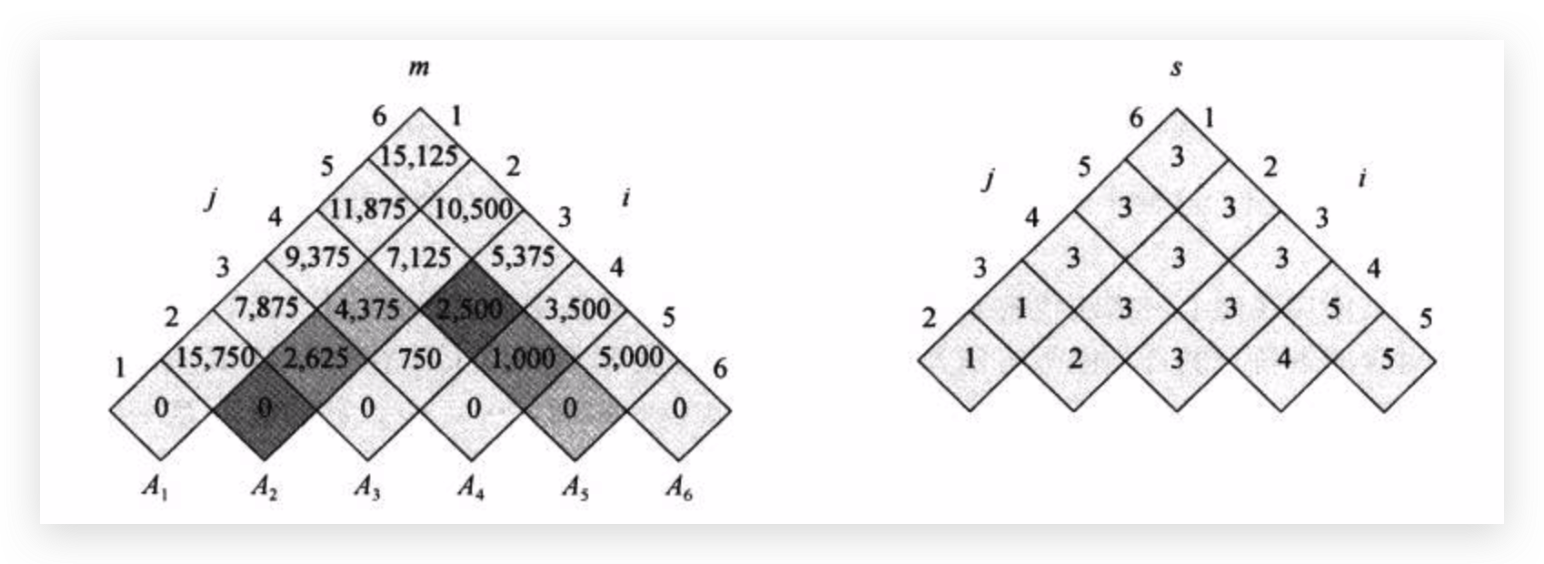
首先是最下面一行,单个矩阵计算量为0,从左到右依次是m[1, 1], m[2, 2], ..., m[6, 6]
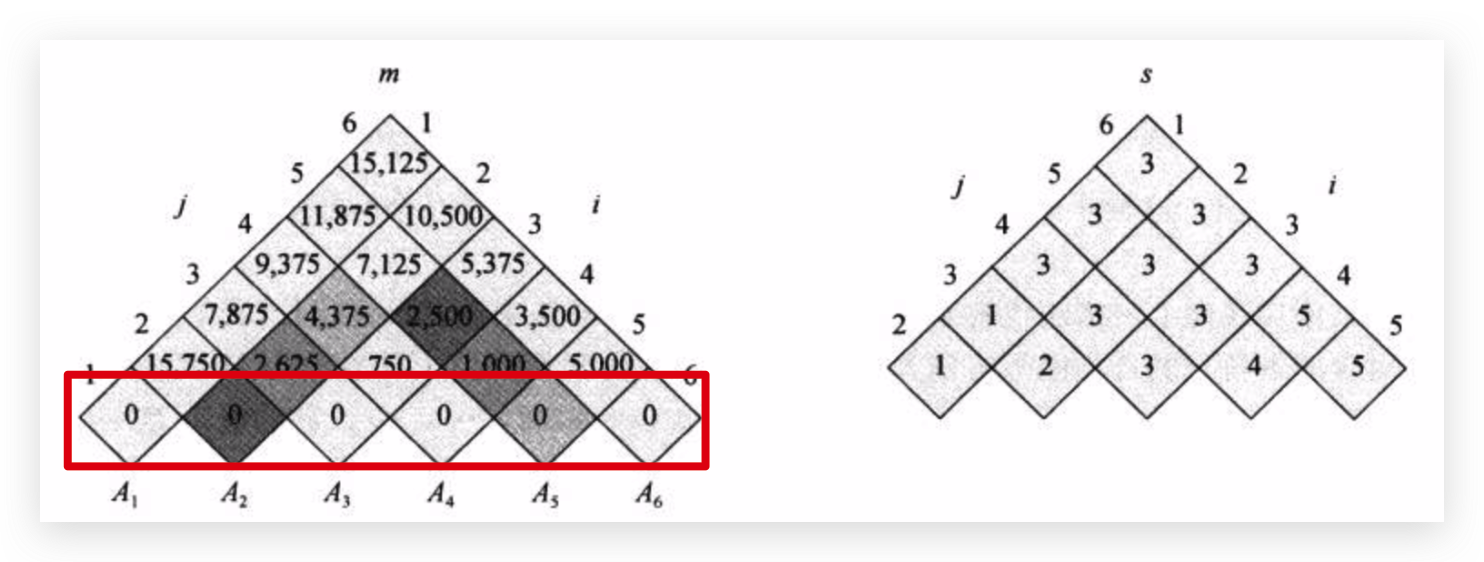
第二行,表示2个矩阵的计算量,使用上面的递推公式求得: \[ m[1, 2] = min_{1 \leq k < 2}(m[1, k] + m[k + 1, 2] + p_{0}p_kp_2) \] 这时候k除了1别无他选,所以 \[ m[1, 2] = m[1, 1] + m[2, 2] + p_{0}p_1p_2 = 0 + 0 + 30 \times 35 \times 15 = 15750 \] k取1,所有右边三角,i=1,j=2时取1
后面的也是这样求解
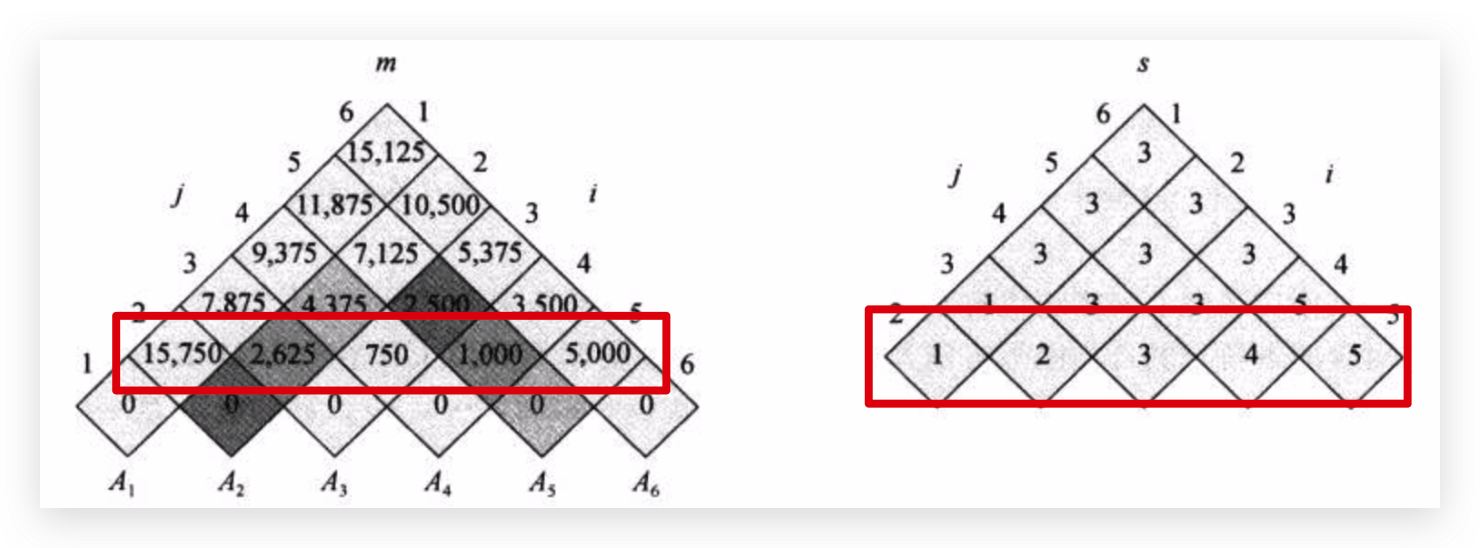
第三行举一个m[2, 4]这个例子 \[ m[2, 4]=\min\left\{\begin{matrix} m[2, 2] + m[3, 4] + p_{1}p_{2}p_{4} &= 0 + 750 + 35 \times 15 \times 10 = 6000\\ m[2, 3] + m[4, 4] + p_{1}p_{3}p_{4} &= 2625 + 0 + 35 \times 5 \times 10 = 4375 \\ \end{matrix}\right. =4375 \] 最佳切分点为3,k取3
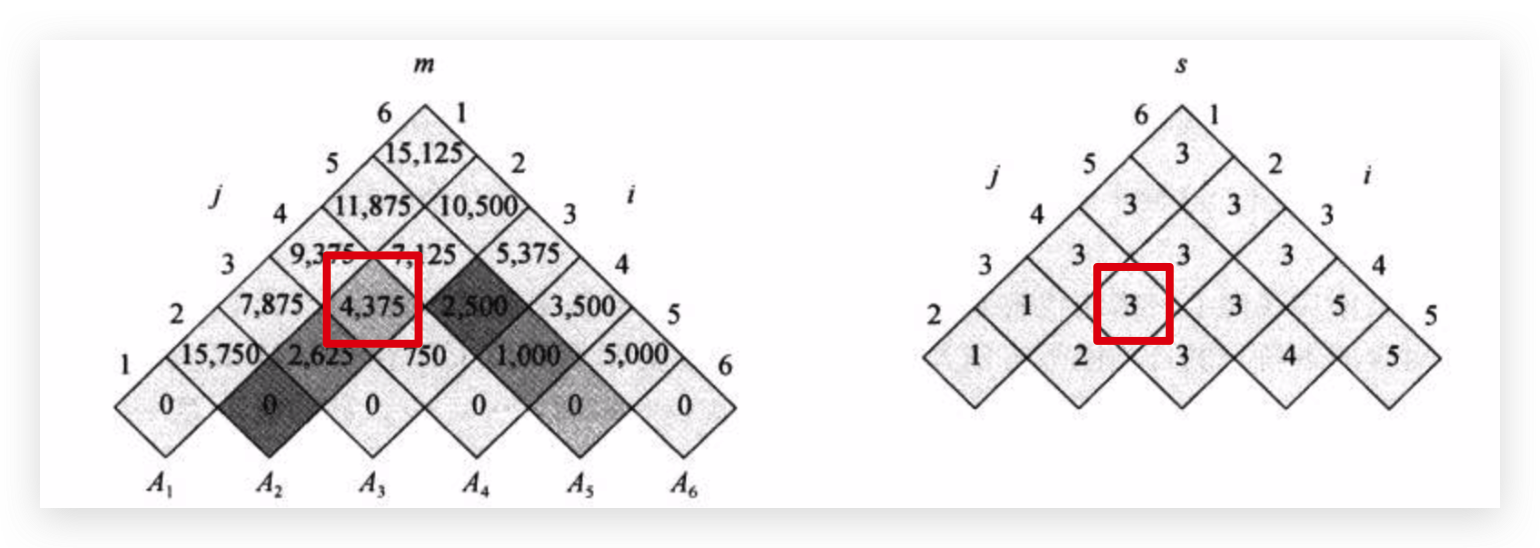
第四行举一个例子 m[2, 5]
 最佳切分点为3,k取3。
最佳切分点为3,k取3。
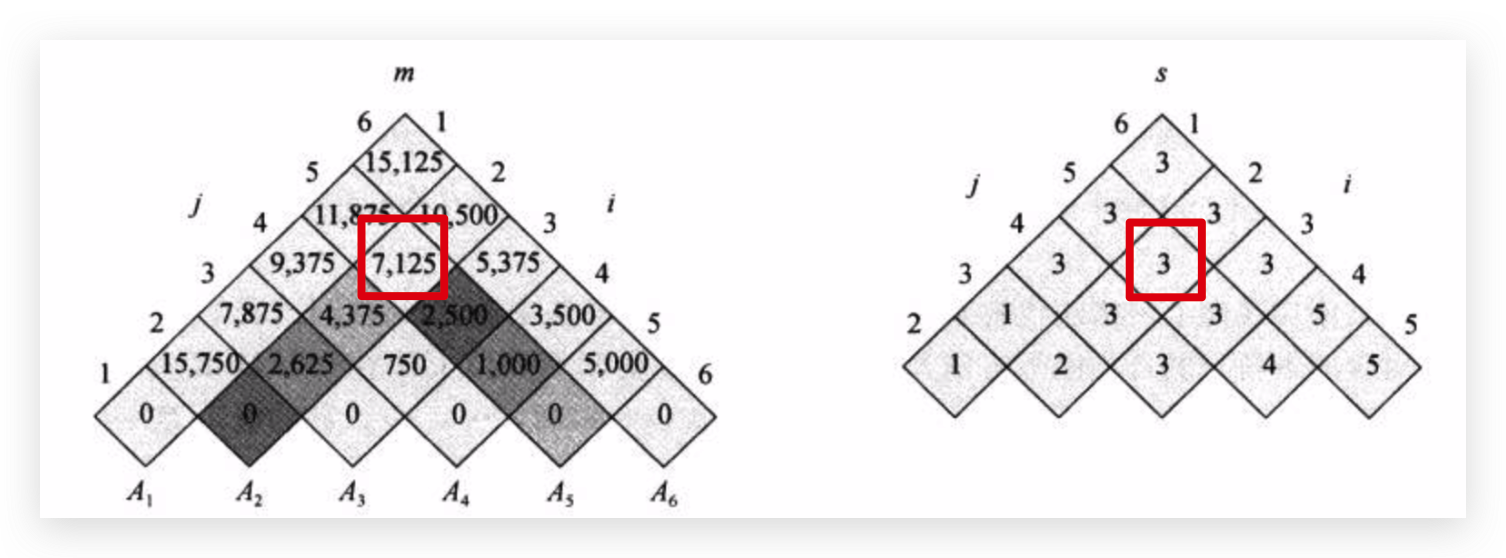
这样使用递归式逐行计算,填满整个矩阵,最顶端的数值就是所求。
代码
1 |
|
练习2 - [编程|100分]最少次数
1 | 时间限制:C/C++1秒,其他语言2秒 |
本题可使用本地IDE编码,不做跳出限制,编码后请点击“保存并调试”按钮进行代码提交。
题目描述
给定一组非负整数,我们最初处在这个数组的起始位置(index=0)。数组中每一个数字代表你可以向数组前前进的长度。求解可以前进到数组末端的最少次数。假设给定的数组可以保证你能够到达数组末端。
输入描述
多行输入,给出n (n <= 10000001)个非负整数,数字由逗号分开且逗号跟数字有任意空白字符。
输出描述
一个数字,表示答案。
示例1
输入输出示例仅供调试,后台判题数据一般不包含示例。
输入
1 | 2, |
输出
1 | 2 |
说明
index0允许我们前进2步以内。第一次从index0前进1步到index1,第二次从index1前进3步到index4 , 完成任务。
题解
分析
最优子结构
题目要求求得可以前进到数组末端的最少次数,也就是从index 0到index n-1(数组最后一个元素),前进的最少次数。
那么可以发现这个问题是有最优子结构的。
现在从0到n-1找一个中转点k,只有当0到k的前进次数最少,k到n-1的前进次数最少,那么从0到n-1的前进次数才能最少。
如果不找这个中转点k,直接从0到n-1呢,根据题意,这时要考虑index0时可以前进多远距离。如果index允许前进的步数大于index0到index n-1的长度,即可以从index0直接跨到index n-1,那么就只需要1步,否则就不可能跨过来。
递推式
\(steps[i,j]\)表示起点为index i,终点为index j,至少需要多少步。 \[ steps[i, j]=\left\{\begin{matrix} 0 & \text{if i = j}\\ 1 & \text{if i < j and be allowed directly from i to j}\\ min_{i < k < j}(steps[i, k] + steps[k, j]) & \text{if i < j and not be allowed directly from i to j}\\ \end{matrix}\right. \]
代码(仅处理输入输出)
1 |
|
例题:最长公共子序列问题 - Longest-Common-Subsequence Problem
题目

题目大意:给定序列X和Y,求出X和Y的最长公共子序列Z。
最长公共子序列定义:
- Z中的元素都在X和Y中出现过
- Z中的元素在X和Y中可以不连续出现
- Z中的元素在X和Y中出现顺序要相同,即在Z中a在b之前出现,那么在X和Y中,a也要在b之前出现

分析
最优子结构性质
如果按照切钢条问题和矩阵链乘法的思路来分析LCS问题的最优子结构,那么可能会这样思考:
若序列\(X\)和序列\(Y\)的最长公共子序列为\(Z\),那么把\(X\)拆成\(x_1\)和\(x_2\),\(Y\)拆成\(y_1\)和\(y_2\),\(x_1\)和\(y_1\)的最长公共子序列是\(z_1\),\(x_2\)和\(y_2\)的最长公共子序列是\(z_2\),把\(z_1\)和\(z_2\)相组合即可得到需要求的\(Z。\)
但是这样切分有时会出问题(绿色的线表示切分):
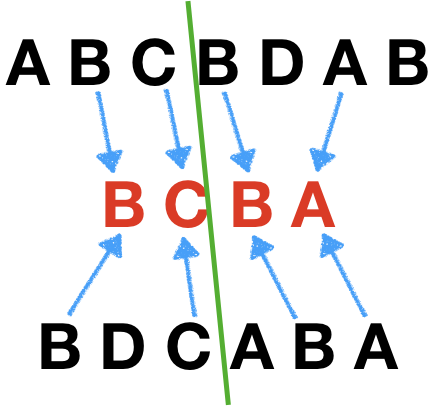
这样就没啥问题,最长公共子序列是BCAB。
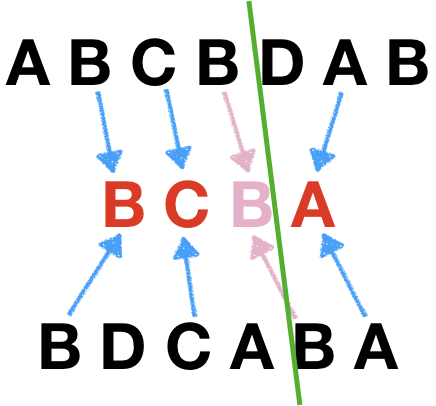
但是如果Z中一个元素被切到了不同的一遍(如上图紫色箭头的部分),就会出问题,最后合成的最长公共子序列是BCA,丢了一个B
但是又很难保证Z中的元素都被切到同一边,所以不采用这种最优子结构的思路。
在最长公共子序列问题中,引入前缀序列这个概念:
给定一个序列: \[ X=<x_1, x_2,...,x_m> \] 对于\(i=0,1,...,m\),定义X的第\(i\)前缀为: \[ X_i=<x_1, x_2, ...,x_i> \] 例: \[ X=<A,B,C,B,D,A,B> \] 则有: \[ X_4=<A,B,C,B> \] \(X_0\)为空串。
现在有\(X=<x_1, x_2,...,x_m>\)以及\(Y=<y_1, y_2,...,y_n>\),最后求得的最长公共子序列\(Z=<z_1, z_2,...,z_k>\),那么最优子结构是:
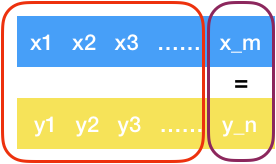
如果两个序列最后一个字符相同,即\(x_m=y_n\)
则最后一个字符一定在最长公共子序列中,也就是\(z_k=x_m=y_n\)现在只需要求\(X_{m-1}\)和\(Y_{n-1}\)的最长公共子序列即可;
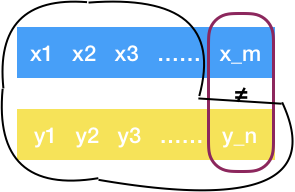
如果两个序列最后一个字符不同,即\(x_m \neq y_n\),则\(x_m\)和\(y_n\)最多只有一个在最长公共子序列中
若\(z_k=x_m\),那么原问题等价于求\(X\)和\(Y_{n-1}\)的最长公共子序列
若\(z_k=y_n\),那么原问题等价于求\(X_{m-1}\)和\(Y\)的最长公共子序列
若\(z_k\neq x_m\)也\(z_k\neq y_n\),那么原问题等价于求\(X_{m-1}\)和\(Y_{n-1}\)的最长公共子序列
但是不需要分这么多情况,只需要分别求解\(X\)和\(Y_{n-1}\)的最长公共子序列和\(X_{m-1}\)和\(Y\)的最长公共子序列,再比较两个求出来的结果,取更长的那个作为原问题的解。
构造递归解
令\(c[i,j]\)表示\(X_i\)与\(Y_j\)的最长公共子序列的长度。
根据上面的最优子结构分析,可得 \[ c[i, j]=\left\{\begin{matrix} 0 &\text{if i = 0 or j = 0}\\ c[i-1, j-1]+1 &\text{if i, j > 0 and $x_i=y_i$}\\ \max(c[i, j - 1], c[i-1,j]) &\text{if i, j > 0 and $x_i \neq y_i$}\\ \end{matrix}\right. \] 第一行为程序的底,如果X和Y中有一个序列长度为0,那么最长公共子序列长度也为0。
自底向上设计程序
使用二维数组记录下dp的结果,这个二维数组i轴表示X序列,index为\(i\),表示\(X_i\),即X序列的前缀子序列,同理j轴表示Y序列,index为\(j\),表示\(Y_j\),即Y序列的前缀子序列。

初始化,第一行第一列都初始化为0,因为若两个序列中有一个序列为0,则最长公共子序列的长度一点为0;
根据递推式:
如果\(x_m=y_n\),则\(c[i, j]=c[i-1, j-1]+1\)
如果\(x_m \neq y_n\),则\(c[i,j]=\max(c[i, j - 1], c[i-1,j])\)
最后右下角的格子里存的就是整个X和整个Y的最长公共子序列长度,每个斜向上的箭头,就是最长公共子序列里的元素。比如上图的元素就是BCBA
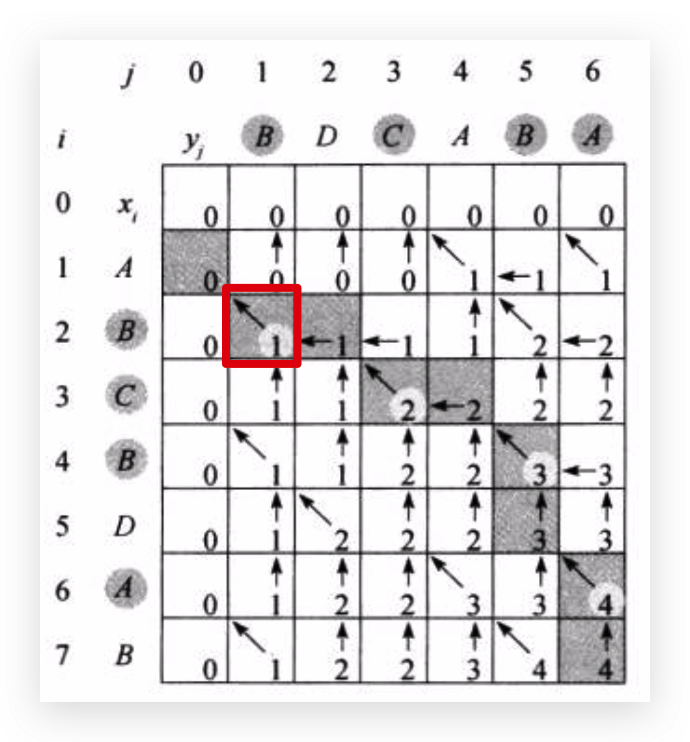
这个格子里,\(x_i=y_j\),都为字符B,所以\(c[2,1]=c[1,0]+1\)
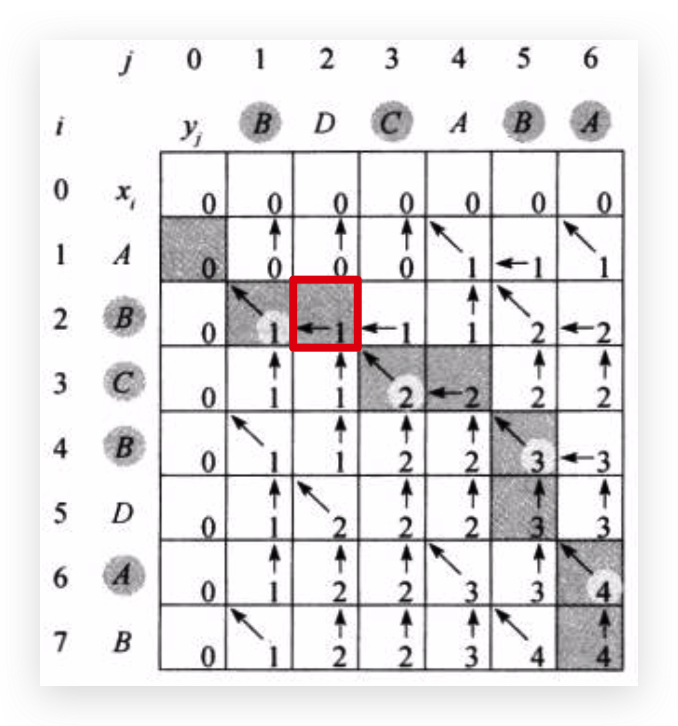
这个格子里,\(x_i \neq y_j\),字符不同,所以取\(c[2,1]\)和\(c[1,2]\)中的较大值,放入\(c[2,2]\)中。
依次类推,求出每个格子里的值,右下角的值是XY完整序列的最长公共子序列长度。
代码
1 |
|
