修塔游戏

Posted on Edited on In Views:

个人觉得比较难的一道笔试算法题，不能直接套用任何一种算法解决，挺有复题价值的~

题目

题目描述

小柯正在玩一款修塔游戏：系统中有n座高塔，每座高塔由若干个高度相同的方块堆砌而成。修塔游戏的规则为:

  1. 每次从最高塔的塔尖拿走一个方块
  2. 每次在最低塔的塔尖堆砌一个方块

小柯每次只能完成上述两个动作中的一个动作。游戏的目标是使n座高塔中至少有k座高塔的高度相同，请问小柯最少需要多少次才能完成游戏。

输入描述

输入共有2行，第一行为n和k(1≤k≤n≤200000 )， 第二行为n座塔的高度组成的数组a1, a2, …,an（1≤aj≤10000）。

输入描述

输出值为最少需要多少次动作才能完成游戏。

示例

输入

1
2
6 5
1 2 2 4 2 3

输出

1
3

分析

这题还是一道搜索类型的题目，最终要求使得n座塔中，k座塔的高度相同。这k座塔高度只要求相同，并没有要求具体高度，这里就需要搜索出最终的高度。

假设最终有k座塔高度相同，他们的高度都是u，u的取值范围一定是[min_num, max_num]，也就是所有塔中的最小值和最大值。因为我们只能对最小值+1，对最大值-1，所以u的高度跑不出这个范围。

既然u的范围确定了，那么可以这样思考。我们遍历每一种可能，也就是尝试每一种u，看看哪一种可能下操作次数最少。可以写一个for循环，循环里的u都是确定的，看看需要多少次操作，可以把n座塔中k个塔高度改为u。

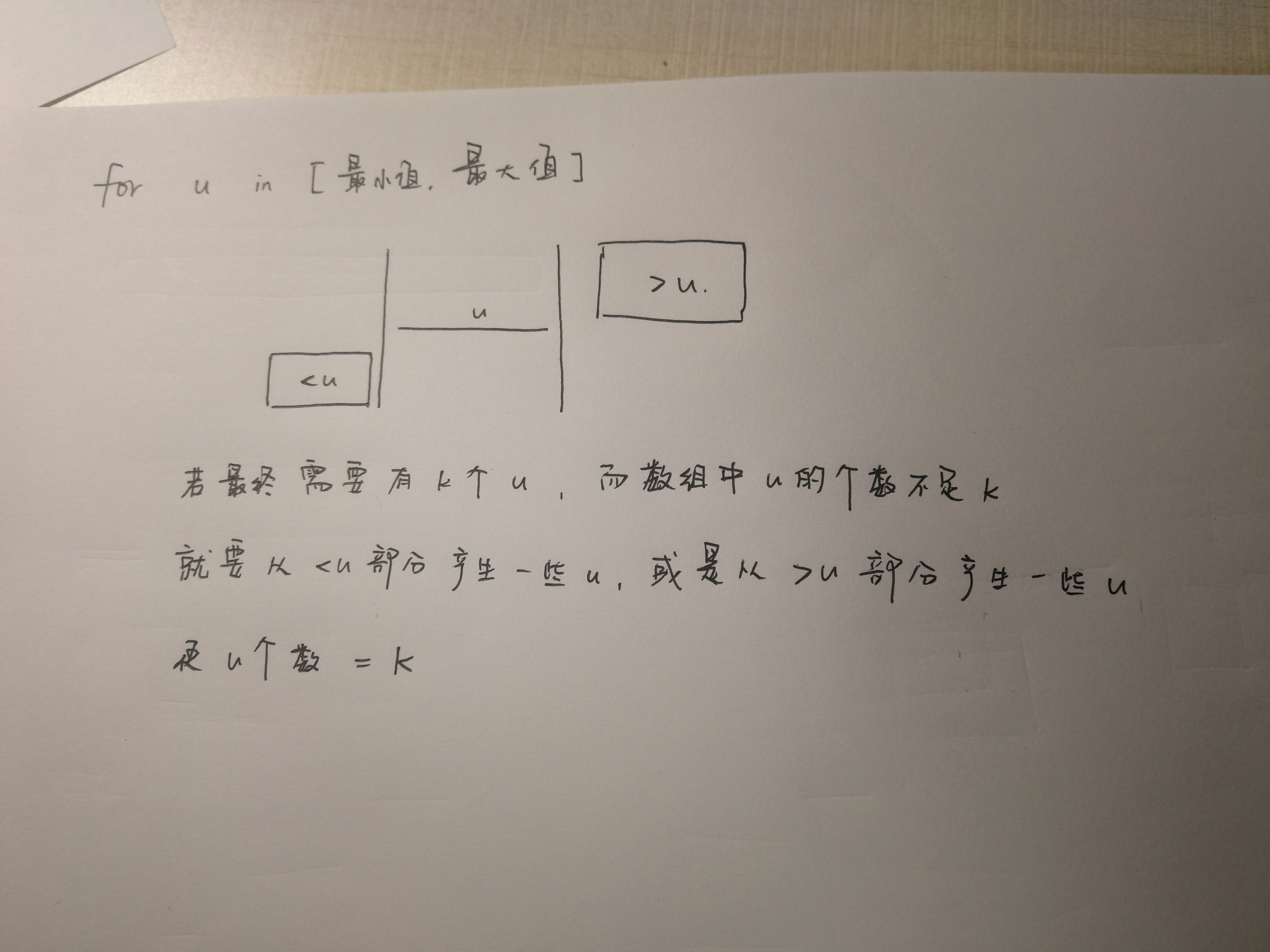
对于确定的u，我把数组分为三部分，一个是<u部分，这里所有的数都<u，一个是=u部分，就是高度为u的数，还有>u部分，这里所有的数都>u，如图所示：

474610307b97518f2844443dec56578

如果我们需要k个u，而=u部分个数不足k个，那么我们就需要从<u部分产生一些u，或者是从>u部分产生一些u。

这里的分配方式可以用穷举的方式来，然后再加上一些限制条件，比如<u部分就2个数，要产生3个u是不可能的，在代码中也加入了这种限制条件。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

int main()
{
    // freopen("1.txt", "r", stdin);
    int n, K;
    cin >> n >> K;
    // count_num 是计数器，记录每个数出现多少次
    int count_num[10001] = {0}, temp;
    // max_num和min_num记录出现过的最大数和最小数
    int max_num = 0, min_num = 20000;
    // 记录数据
    vector<int> num(n);
    for (int i = 0; i < n; i++)
    {
        cin >> temp;
        num[i] = temp;
        // 记录出现次数
        count_num[temp]++;

        // 维护max_num和min_num
        max_num = temp > max_num ? temp : max_num;
        min_num = temp < min_num ? temp : min_num;
    }

    // 将num数组从小到大排序
    sort(num.begin(), num.end());

    // 对于固定的u，把所有<u的数经过+1操作变为u-1，需要left_process次操作
    // 对于固定的u，把所有>u的数经过-1操作变为u+1，需要right_process次操作
    int left_process = 0, right_process = 0;

    // 有 left_count 个数小于u
    // 有 right_count 个数大于u
    int left_count = 0, right_count = 0;

    // 初始化right_process和right_count，把所有>u的数都降成u + 1需要多少次操作
    for (int i = 0; i < n; i++)
    {
        if (num[i] > min_num)
        {
            right_process += num[i] - min_num - 1;
            right_count++;
        }
    }

    // 对于数u，<u的部分负责产生left_num个u，>u的部分负责产生right_num个u
    int left_num = 0, right_num = 0;

    // <u部分产生left_num个u，需要cur_left_process次操作
    // >u部分产生right_num个u，需要cur_right_process次操作
    int cur_left_process = 0, cur_right_process = 0;

    int min_process = INT_MAX;

    // 遍历所有可能的u，范围是 [min_num, max_num] 区间
    for (int u = min_num; u <= max_num; u++)
    {
        // 分配 <u 部分产生left_num个u，相应的 >u部分就要产生right_num个u
        // 加上一些限制条件，left_num <= left_count 意思是 <u部分 产生的u不能超过 <u部分的总个数
        for (left_num = 0; left_num + count_num[u] <= K && left_num <= left_count; left_num++)
        {
            // 同样对 right_num 的约束
            right_num = K - left_num - count_num[u];
            if (right_num > right_count)
                continue;

            // 如果 <u 部分不需要产生 u，那么操作数为0，否则要将左边数先都变为 u - 1，然后需要多少个u就加多少操作数
            cur_left_process = left_num > 0 ? left_process + left_num : 0;
            // 右边同理
            cur_right_process = right_num > 0 ? right_process + right_num : 0;

            // 记录最少操作数
            min_process = cur_left_process + cur_right_process < min_process ? cur_left_process + cur_right_process : min_process;
        }

        // 当遍历下一个u时，也就是u要变成u+1了
        // 我们要把所有u - 1的数加为u，left_process要增加 <u的个数，也就是left_count个
        left_process += left_count;
        // left_count 要加上有多少个u
        left_count += count_num[u];

        // >u部分同理
        right_count -= count_num[u + 1];
        right_process -= right_count;
    }

    cout << min_process << endl;
    return 0;
}

Image